Hi, high current amplifier is one that is designed to deliver large amounts of current (amperes), when needed, typically low impedance speakers. They have very robust power supplies -- i.e. large transformers, capacitor banks, high-performance transistors, etc.
Specs such as doubling (or near doubling) power as impedance halves, big cooling sinks for heat dissipation are telltale signs of high-current designs.
If oyu have low impedance speakers or listen to dynamic music (e.g. orchestral) you need such an amp.
Most high-end amplifiers are high current, some higher than others. Tytpically, Krell, Symphonic Line, CH Precision, Boulder, FM Acoustics, Vitous, Gryphon, etc are high current.
|
Let me start from the easiest of your questions: power consumption is largely irrelevant to the issue (except... more on that later).
The relevant value for E (or V) is the internal voltage of the amplifier power supply, not what comes out of the wall socket/receptacle. That 'E' is specified to provide a certain amount of power to a load, which in domestic audio is generally taken to be an 8Ω resistor. Hence the typical specification of (say) 50 Wpc/8Ω.
Note that in a resistor, electromotive force and current are linked by Ohm's law, which says:
E = I * R (where R is the resistance)
now, if you replace that into the 'PIE' equation, you get:
P = E²/R = I²R
so, assuming a load of 8Ω, a 50 wpc amp has to provide
E = √(50*8) = 20 V of internal voltage
I = √(50/8) = 2.5 A of load current
So far, so good; the designer specifies a power supply and final stage that can provide 2.5 A and 20 V, and everyone is happy.
The problem - and it can be a problem - is that loudspeakers are not resistors: the 'resistance' (more appropriately impedance) they present to an electrical current varies with the frequency of the input signal, and it can be much lower or higher than the nominal (most commonly 8Ω or 4Ω) at certain frequencies.
For example, let's assume that speaker X has a minimum impedance of 2Ω at 200 Hz, vs. a nominal impedance of 8Ω (usually at 1 kHz). What happens to the current then, when the amplifier is fed a 200 Hz input signal such that the output is driven to its maximum?
Well, the voltage is still going to be 20V, and Ohm's law still applies:
I = E/R = 20/2 = 10A
That's four times our initial specification. This can spell trouble for both the power supply and the final stage, particularly if this is sustained over significant periods of time. The designers can take precautions (protection circuitry) to prevent damages, but that may mean sound quality degradation and/or shut-down.
Alternatively, the designers can incorporate in the specification the ability to provide (at least temporarily) much higher currents than the standard, continuous Wpc/8Ω would imply. This is a 'high current amp'.
Where does 'consumption' power come in? Well, typically that is calculated as the maximum (continuous) power that the amp will draw - note that in the case above (E = 20V, R = 2Ω), P = E²R = 200W
If the amp is capable of providing indefinitely 200W to a 2Ω load, then the consumption power has to be at least that much (plus inefficiencies and 'overhead' power needed to manage other functionality e.g. power meters, lighting).
Finally, an example of a high current amp - Accuphase E800 (50 Wpc/8Ω; 100 Wpc/4Ω; 200 Wpc/2Ω; 300 Wpc/1Ω). A low current amp - AudioNote P1 (9 Wpc/8Ω; 9Wpc/4Ω; no information on lower loads, but, given the design, power is likely to go down rather than up). Note that what matters is not the 'starting number' of Wpc, but how much they go up - or not - with decreasing load impedance.
There's a lot more to explore on amps design and power specifications, and the above is necessarily approximate, but I hope this short novel at least answers your initial questions.
|
A Coda 16 has 280,000 uF of capacitance and can deliver 100 amps of current, per channel.
A Gryphon Essence stereo has 440,000 uF, so can probably deliver more, note that is described as a 50 wpc amplifier.
Going off the top of my head, I recall many years ago that a low end Sony home theatre receiver was labeled as a 100 wpc 5 channel receiver. When actually tested with all 5 channels running it produced 15 wpc. It probably had the same power supplies as a modern audiophile level DAC, needless to say it was not a high-current design.
|
I didn't read the wordy versions above, or I quit at the first incorrect statement in each of them. Here is the simple version:
Amp WPC is a rating taken at nominal resistance, that is, optimal conditions.
Now if resistance goes down, to keep voltage constant, amperage has to go up. If amperage can't go up (low current amp), then voltage, and therefore power, will be limited by the capability of the amp. thus you need an amp capable of providing high current for speakers with low impedences.
Jerry
|
"And lastly, what would be an example of a high current amp and what would be an example of a low current amp?
Thanks."
My take;
If you’ve got a bunch of big honkin’ capacitors in your amp, you’ve got a high current amp.
If you don’t, you’ve got a low current amp.
Hope that’s not too highly technical for everyone!😃
|
Not only low impedance but impedance curves matter greatly as well.
|
Your understanding of the electrical formulas are correct. Impedance curves are most easily obtained from Sterephile reviews, such as this one. The top chart shows an impedance curve.
This particular speaker shows a minimum impedance ~ 6 Ohms, and IMHO would be a good candidate to be called an 8 Ohm speaker.
I also want to caution you that I've seen dynamic speakers designed specifically to be hard to drive. They are sold as "revealing of an amplifier's capabilities." Well, that's great but it doesn't help them play music.
Of course, some speakers just have bad crossovers, and some like the Apogees or electrostatics just can't help it.
To add to your electrical understanding, amplifiers have an output impedance that is also not usually flat. Often they are better in the mid to bass than the treble. That's something else that should be considered. ESL's are hard to drive in the treble. A "weak" amp will lose treble output.
|
@gregm +1
High current is shorthand for delivering more current on demand. The P=IE formula remains the same.
An imperfect analogy would be gas engines. A Ford F-350 will go 60 mph. A Ford Fiesta will also go 60 mph. When towing a trailer with a 2 ton load, the F-350 will deliver more power on demand than the Fiesta. When going uphill, there will be less strain on the bigger engine – while the smaller engine might crap out.
Some speaker designs have low impedance dips at certain frequencies which require more instantaneous current delivery. The goal is to reproduce the authentic sound of the musical instrument: such as a thwack of a snare drum, the gut punch of a kickdrum, the shimmering of cymbals or the blaaat of a trumpet.
Matching the speaker and the amp is important. This is where transient response is involved.
|
@mclinnguy This statement is false:
A Coda 16 has 280,000 uF of capacitance and can deliver 100 amps of current, per channel.
Here’s why. As @immatthewj points out, the power the amp makes is equal to the current times Voltage. The actual Power formula is 1 Watt= 1 Amp x 1 Volt; IOW power is equal to Volts x Amps. A derivative of this formula that includes Ohms is Power= Ohms X Amps squared.
Giving the Coda the benefit of the doubt, that it can drive a 1 Ohm load, at that impedance the power is equal to the amperage squared. So I think you can see the Coda, as good as it is simply can’t do that; that’s 10,000 Watts! That sort of current through the output section of the Coda would heat the output devices to slag.
That value is actually the amount of current that flows when the power supply is shorted for 10milliseconds so has nothing to do with output power nor the impedance it can drive.
My take;
If you’ve got a bunch of big honkin’ capacitors in your amp, you’ve got a high current amp.
@thecarpathian Please read my above explanation about why this isn’t true. The reason to have lots of capacitance in the output section is to prevent the amplifier from modulating the power supply which can introduce IMD. It has nothing to do with the output power otherwise. We make some amps that have large 3" diameter caps which have a lot of storage; as much as any solid state amp of the same power. But being tube amps they are not likely to be considered ’high current’.
What is important for most speakers is that the amp can behave as a Voltage source; IOW that it can produce the same output Voltage regardless of the load impedance. No amp can actually do that of course but over the range of impedances most speaker present there are quite a few amps that do behave as Voltage sources on them.
But to be clear a tube amp can behave as a Voltage source too as long as it has enough feedback to allow for a low output impedance. But instead of doubling power as impedance is halved it cuts power in half as impedance is doubled.
|
@atmasphere ,
I’ve always thought the higher the capacitance reserve an amplifier has, the more amps it can deliver when needed. This isn’t correct?
I read what you wrote, but frankly really didn't understand it!
|
|
I’ve always thought the higher capacitance reserve an amplifier has, the more amps it can deliver when needed. This isn’t correct?
@thecarpathian That isn't correct. By that metric our MA-2 can deliver more amps that most solid state amps of the same power. The output power is determined by the power supply Voltage and the resulting current that the output devices can handle. So that has a lot to do with the power transformer and the dissipation the output devices will see. In short- its complicated.
|
"In short- its complicated."
For me it sure is!
Thank you for correcting my mistake. You guys are light years ahead of me with this stuff.
|
I had thought capacitance had to do with instantaneous current delivery as well.
Obviously 100 amps through a 15 amp outlet is impossible for long periods.
In theory as far as continuous power one can only have 80% of 15 amps x 120 volts = 1440 watts before the breaker trips, assuming the power amp is the only draw on the circuit. I don't know how short this time period is.
But an amplifier is not a hair dryer, and we are not blowing our speakers or our ears with a sine wave.
@atmasphere so what might be the instantaneous currents provided in music reproduction, even for a few milliseconds?
|
so what might be the instantaneous currents provided in music reproduction, even for a few milliseconds?
@mclinnguy The instantaneous power will be within the output power limit of the circuit. Therefore so will the current (else the amp fails or goes into protect mode). Generally speaking its not that much! On a 4 Ohm non-inductive load 200 Watts will produce roughly 7.07 Amps (200 = 4 times the current squared; IOW the square root of 50). If there's a weird phase angle involved with that impedance in a nutshell it will behave as if the load impedance is lower. So if similar to 2 Ohms then the current is 10 Amps.
So you can see all these wild current claims are not having to do with output power that's actually driving the speaker.
|
@dlevi67 +1
amp does deliver current to speaker-load, AND also dampens / controls current from speaker (inductors and capacitors in passive crossover, inertia generated current by drivers), thus higher current than just driving resistive load output stage is needed.
|
@atmasphere ,
One more quick question:
What do you mean specifically when you say ’output devices’? The amp itself or certain components within the amp?
Thanks
|
@thecarpathian 'Output devices' means components in the output section of the amplifier; usually power transistors mounted to a heatsink. We make both class D amps and tube power amps so in their cases either GaNFETs or power tubes.
|
@atmasphere
Thanks again.
I don’t know if you get told this often, but I really appreciate that you take the time out from what I’m sure is a full dance card to offer your insight here and to educate.
|
Some amplifier manufacturers do take current measurements on the outputs of the amp, the Krell I400 has 62 amps of peak current on the output. I'm sure those are taken for only brief milliseconds before the outputs fry.
|
@gregm , @steakster
+1
Amps measure the provided flow of electric current.
Watts measure the amount of electrical power being used.. Watts are calculated by multiplying the current in amps by the voltage of the source.
Sufficiently beefy amps needed are dependent on the speakers you are running. A high-current amplifier is simply one in which it has a robust power supply and output stage that can pass enough current to drive low-impedance loads. If you have 4 ohm speakers that might drop down below that at times, you’ll need something with a fair chunk of available and fast delivery of current to run them decently.
To deliver large amounts of current, you need a beefy power supply (or plural independent channel power supplies) with multiple output device pairs, and GOOD heat sinking. The amplifier can be class A, AB, B, D, whatever...
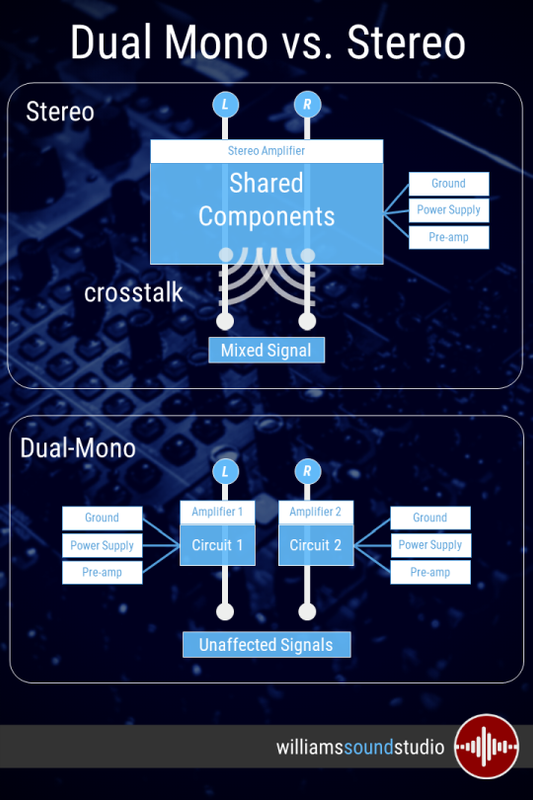
The top end build (…and price ) amplifiers are “ dual mono”. amplifiers.
- A dual-mono amp contains two mono channels that are independent of each other.
-A simple stereo amp consists of two shared channels which always share a single common power supply and thus are always dependent on one another.
Essentially, in a dual-mono setup, these are two separate amplifiers with the same design, with matched or high manufacturing tolerance (read: more expensive) components. The pic below (Dual-Mono) shows that the left and right signal paths are entirely independent of each other ….each with their own independent high-end , robust & beefy power supplies.
WHY WPC Ratings can be misleading and prone to marketing crap Now ….. think multichannel AVR’s that share a single power supply for all its channels with a stated, say, 100 wpc rating, ….. The big power sharing between channels dilution is obvious .
The stated marketing blurb of quoted number wpc without reference to the available current delivery and other output metrics is now split across all the channels, Each channel that an AV receiver supports will need the power to run. The more channels you have, the more power-hungry the AVR will be to make full use of its capabilities.Thst is why most AVR’s flunk out in 2 channels optimal performance as underpowered units that fail the performance of the speakers.
The FTC 1974 Rule? If a standard is selected and adhered to by all, then at least we’d have a method of comparing products in terms of their available power output on a fair basis.
More than 50 years ago, before the arrival of surround sound and multichannel products, there was a universal standard set up by the Federal Trade Commission (FTC), which established a method for rating stereo (two-channel) receivers and amplifiers.
The FTC’s 1974 rule specified that stereo amplifiers be rated with both channels driven simultaneously into 8 ohms across a specified bandwidth (20 Hz to 20 kHz) at a specified level of distortion (THD), and that’s how things went until the appearance of multi-channel AV receivers.
Some real life examples of the fallacies on current AVR power ratings re: WPC as a true measure of amp power
120 watts per channel; all channels rated at 0.05% THD”
(no bandwidth mentioned; no impedance load, no mention of any channels driven simultaneously)
“7 x 125 watts per channel”
(No frequency range stated, no distortion rating, no mention of number of channels driven, no mention of impedance load)
“Front L + R: 85 watts per channel, 20 Hz to 20 kHz, at 0.08% THD, into 8 ohms, both channels driven.”
(Very good ratings for two stereo channels; other channels were similarly specified, in pairs, but no ratings for all channels driven)
“No power output specified”
(unbelievable!)
“100 watts per channel x 7; 20Hz — 20 kHz; 0.03% THD, 8 ohms; all channels driven”
(Excellent but still needs each channel’s maximum output)
Except for the last unit, a lot of confusion ensues about exactly what sort of per channel output capabilities each receiver has.
tt should be stated that no matter how you decide to test an AV receiver’s amplifier output section, it will always involve a test signal that bears little relation to music signals from a CD, DVD, or other source.
Music signals, by nature, are always varying, not just in level but also by frequency, so it’s impossible to generate a test signal that exactly duplicates music or soundtrack signals since they vary every moment.
TAKEAWAY
Difficult speakers needing “ grunt” to drive means a beefy need for amperes (current) ….not just confusing WPC ratings in isolation.Match your amplifier accordingly wisely.
|
|
Those are formulas for static case, i.e. single wave. But is amp capable of delivering a lot of current on high transients QUICKLY? It may be high current capable when single is stable, but what about transitions (which is what music is)? Is it able to raise current and provide energy fast enough?
|
Thank you to @everybody for the great feedback!!!!
I am going to try to simplify what I think I got out of the answers that were generously provided, and see if I've got it:
C WPC are a product of the voltage that the power supply supplies x the current. The amp could be rated at a certain amount of WPC but if the current dropped off whenever it (the amp) encountered a significant drop in impedance then the amount of wpc that it was theoretically rated as putting out would also drop way below what it was rated at? Unlike a "high current amp" in which the current would not drop so therefore the wpc would remain constant?
(So would this mean that the rated wpc is almost meaningless if the current isn't enough to sustain that wpc?)
So if I have that right, does the 4 ohm tap have any bearing at all on whether the amp is a high or low current amp?
And would there be a specification listed that would tell me how an amp stacks up as far as the amount of current?
Again, thanks for all the input, it is greatly appreciated!
|
Excellent and informative discussion. Thanks to all even if it is a bit tough for dummies like me to understand
|
How does any of this inform a future purchasing decision or help us enjoy what we have now?
|
Amplifiers are not about power. Power is consumed by the load, whether it's a resistor, a motor or a speaker driver. The amplifier is an energy source and does not necessarily follow Ohm's Law. As an example, if you short a 9-volt battery with a 1/2-ohm resistor, Ohm's Law dutifully informs us that the "power" delivered is 162 watts (9Vx9V/0.5) and the current is 18 amps. Of course that is ridiculous; the energy storage of a 9V battery is limited to about 500 milliamps and only when a resistor limits the battery to less than 500mA does Ohm's Law apply. On the other hand, that 150kVA utility transformer feeding your street can easily slam thousands of amps over a bolted fault. It's all about energy.
An amplifier has an energy source: the power supply's transformer and filter capacitors. If the power supply can maintain it's secondary voltage from any load the speaker presents it, you can call it a "high current amplifier" and relationships established by Ohm's Law apply. But if the output voltage sags when the speaker load drops, then the current delivered to the speaker will decrease, which means the power consumption decreases.
If an amplifier's specs says it can maintain voltage down to 4 and/or 2 ohms, you will see the power double (i.e. 100W into 8 ohms, 200W into 4 ohms and 400W into 2 ohms) and that is practically a true voltage source. But if you see 100W into 8 ohms and 150W into 4 ohms, then that amplifier is not as good of an energy source.
|
Uhm - Ohm’s law applies regardless (or its generalisation using impedance). It’s just that at some point the internal impedance of the generator (amp or battery) becomes relevant and has to be included into the circuit being analysed explicitly, rather than neglected.
|
Ohm’s law is one of the simplest laws of physics, yet seems to be so hard to apply properly.
What matters is the voltage drop across the load, Multiply this voltage drop by the current flowing, and you have the power (or Wattage) produced at the load.
The current that flows is just given by the relationship voltage drop = current times resistance.
Amplifiers might be considered to be ’straight wires with gain’ to quote Peter Walker of Quad. They try to produce an output voltage which is a multiplier (the gain) of the input signal voltage. So the voltage drop is given by the input signal and the gain, and the resistance is also fixed (at least nominally).
If the rated maximum power into 8-Ohms is say 100-Watts, that must be the voltage drop times the current. The current is the voltage drop divided by the resistance. So 100 = V * V / 8 or V = sqrt (800) or about 28-Volts. Note that this is derived just from the power and the load resistance.
This is true for Direct Current. When we measure alternating currents, it is conventional to think of them as equivalent to the direct current that would produce the same average power. Turns out this is the square root of the average (mean) of the instantaneous value squared. Abbreviated to RMS (root mean squared).
I feel better now ...
|
A lot of good information here. The bottom line for me is to make sure the amp you choose can drive the speakers you choose. A lot of the manufacturers information is misleading because it’s marketing instead of science. Note some of the online reviews that show a speaker’s impedance. The manufacturer will state it’s 8 ohms and when it’s tested It may dip as low as 2 ohms. That means you would want to select an amp that shows it has been rated and has power at 2 ohms. Some amps will only show specs at 8 ohms. If the amp can handle 2 ohm loads the manufacturer will usually publish it because it’s a selling point. That’s one of the reasons I usually only buy equipment I can buy and try in my system and return for no or little cost if it doesn’t sound right to me in my listening room.
|
@atmasphere
Thank you for the lesson, very useful. I was a Ground Radio Repairman in the USAF. My impedance training was focused on matching antennae to transmitters (along with other factors). A visual "test" of radios, like a big SSB, was the size and number of capacitors. We paid attention to impedance matching. Along with the characteristics of the antenna termination... open, capacitance, resistance, inductive , etc. I've forgotten 90% of what I learned (it was so very long ago). But for my humble needs, if the manufacturer lists power output to the speakers as doubling, or nearly so, from 8 ohm to four and again to two ohms, it is a high current amplifier. If you open the hood, large transformers, and large capacitors are a visual clue. Do not get across the terminals of a large cap and ground without discharging the cap. The potential (voltage) can kill, which explains the "No User Serviceable Parts" stickers.
Not just any speaker will perform its best with just any amp.
|
I’ve always thought the higher the capacitance reserve an amplifier has, the more amps it can deliver when needed. This isn’t correct?
@thecarpathian - kind of sort of. Think of the amplifier as a weight lifter, and the power supply as the stage the athlete stands on. The better the power supply, the stiffer the stand and the better the weight lifter is able to dead lift up to the same point.
The capacitance reduces power supply ripple and attempts to feed the amplifier constant DC voltages. That is, how much the DC rails vary based on incoming AC and amplifier demand.
Many things go into what the ideal capacitance levels are. Amplifier feedback, speaker load, etc. Generally speaking though, if you want to design a high current amplifier you will need to add more capacitance to ensure it can perform to spec even during high demand.
Should also point out that most amplifiers use linear, unregulated supplies, meaning they are subject to the long term voltage stability coming out of your wall. Seasons, your neighbors, your HVAC and refrigerator can cause instability even with dedicated lines.
|
|
@erik_squires ,
To your weight lifter analogy;
I would liken the weight lifter to the amplifier, the weight he's lifting to the speakers, and the power supply to how much muscle (power reserves) he has.
Theoretically, the more muscle he has (capacitance), the more weight (low impedance speaker) he can lift with minimal strain.
Is this reasonable? I hope so, because now I need an aspirin...
|
You have brought me back 47 years to college physics with Herr Professor Doctor Weber at Fordham University. I want to thank all of the physicists in the thread for excellent, simplified explanations. Parallel to the OP’s question on current and power is the importance rate at which an amplifier's output voltage can change over time or slew rate. I believe slew rate is important because it affects the bandwidth, performance, and distortion of an amplifier. In my experience I was concerned at first in moving from a 300 watt, high current amp to a 120 watt integrated amp with a smaller power supply transformer to drive speakers that are not efficient by any definition. The integrated amp had better bass and dynamics, including faster dynamic swings. The integrated had a much higher slew rate. Therefore, my conclusion is slew rate is important to SQ, though not as much impedance matching, To the physicists and electrical engineers, is my conclusion valid?
|
|
To your weight lifter analogy;
I would liken the weight lifter to the amplifier, the weight he's lifting to the speakers, and the power supply to how much muscle (power reserves) he has.
Theoretically, the more muscle he has (capacitance), the more weight (low impedance speaker) he can lift with minimal strain.
@thecarpathian
No, I would not, because they are really two units and both have to be up to par.
I'd say the muscles are the output stages (transistors, tubes, etc.) and heat sinks. The power supply is the stage he's standing on. Both have to be strong enough for the weight.
I'm adding heat sinks because they are a major enabler for Class A and A/B designs. You will melt your transistors without adequate heat sinks. Though truth be told the legal requirements to rate an amplifier n Watts may cause many amps to have exaggeratedly large heat sinks for music playing.
|
Now I get why you said it the way you did.
A couple more aspirin and I may have this partially figured out..
|
The topic of "high current" wouldn’t matter if speakers worked like plain resistors - e.g. acting as the same constant 8 ohms value (or 4 ohms, or 2 ohms) at every frequency from 20Hz - 20kHz. But speakers don’t do this; not even close. Hop onto Stereophile’s online archives and look through the measurements for various speaker models - they often include a graph of impedance (ohms) versus frequency. The curves you’ll see are very, VERY far from the straight flat line you’d get from a plain resistor. Of course it’s more complicated than just that, so they also include a phase angle curve.
So what happens when an amplifiers tries to drive one of these "variable impedance" curves? Well, if it’s a:
- "High Current" amplifiers will produce more power into the "dips" of the curve (lower impedance), thus relatively boosting the SPL at those frequencies. The gold standard of these is amps which claim to "double down", which is the theoretical limit for load invariant amplifiers (e.g. produces twice the power into a 4 ohms load verus an 8 ohm load). These amps are also called "voltage sources", becasue their voltage output remains constant (does not dip) while driving loads of increasingly smaller ohms.
- "Low Current" amplifiers (though nobody calls them that) will NOT produce more power into the dips - though in practice they are affected, and will produce some amount that is more or less depending on numerous factors. But they typically will NOT come close to "doubling down". These amps are also called "power sources".
So which is better? It totally depends on how the speaker was designed! The designer has to (somehow) balance these disparete drivers, crossover, and (likely) amplifier behaviors off of each other to produce a result that sounds natural. If they designed with "only" high-current amplifiers, the speaker will surely sound different driven from a tube amp, and vice versa! What’s perhaps surprising is how many speaker models sound good - albeit different - from both high-current SS amps and tube amps.
Most ported speakers will show a HUGE bump in their impedance in the bass region, right around where their actual bass response starts rolling off. That’s due to the port tuning. You’d think this would mean a high current amplifier should sound "anemic" at these frequiencies, from the high impedance (where they produce much less power), but the reality is this bump represents a "resonance" where the speaker system is actually particularly efficient at generating those frequencies. So yeah...a lot of complexity for a speaker designer to juggle...
|
@thecarpathian Maybe an easier analogy is legs vs. arms.
You need both to be able to dead lift.
|
That’s it, I’m out of aspirin...
Plus I use a leg press machine, better on your back...
|
Therefore, my conclusion is slew rate is important to SQ, though not as much impedance matching, To the physicists and electrical engineers, is my conclusion valid?
@jsalerno277 No. Its a lot more complicated than that. Slew rate is only one of 40 or 50 variables that make up sound quality. There are some excellent sounding amps that have very low slew rates.
"Low Current" amplifiers (though nobody calls them that) will NOT produce more power into the dips - though in practice they are affected, and will produce some amount that is more or less depending on numerous factors. But they typically will NOT come close to "doubling down". These amps are also called "power sources".
@mulveling This statement is incorrect. You could be referring to a tube amplifier in this. Tube amps, if imbued with enough feedback, can behave as a Voltage source yet won’t double power when presented with a load of half the impedance. Instead, they will cut power in half when presented with a load of double the impedance. If the tube amp has no feedback, then it will behave more like a power source although it will be only roughly so. If the amp has both current and Voltage feedback and the two are balanced to the same amount then the amp can behave as a true power source. If you did this with a solid state amp it would behave that way too.
At any rate, a tube amp with enough feedback can drive a variable impedance test load with minimal variation- around 1/10dB, yet no tube amp is considered ’high current’.
A better model for a ’high current’ amp is one that can double power from 4 Ohms to 2 Ohms. Whether that’s of any help with most speakers is highly dubious; any power amplifier will sound better (have lower distortion) if its not having to work hard for a living!
|
@thecarpathian
The capacitance reduces power supply ripple and attempts to feed the amplifier constant DC voltages.
Theoretically, the more muscle he has (capacitance), the more weight (low impedance speaker) he can lift with minimal strain.
But I thought when someone was really muscular, they had more ripples? 
|
|
Speakers are current driven complex impedance devices. They are not a purely resistive load. Because of that complex impedance speakers require more current at some frequencies tha others.Ohms law applies, but only at a given frequency will the calculations be accurate.
Amplifiers ability to deliver current to loudspeakers is gated by the current carrying capacity of the output stage transistors or tubes and what the power supply can deliver.. Bigger power supply caps simply give more reserve under demanding loads within the limits of the output devices.
To protect the output stage, some manufacturers implement current limiting that prevents the amp from trying to deliver more current than the output stage can safely deliver. This happens especially at low frequencies and high volumes, but the audible impacts are throughout the spectrum.
Power supplies, especially the capacitors, and the output transistors are the most expensive components in an amp. This why 'watts per dollar' is a terrible metric it inevitably leads to amps that measure well on the bench, but donr sound very good, especially when pushed, or when driving demanding speakers.
Finally speakers generate their own current, called 'back EMF' when a coil moves in a magnetic field. This has to be absorbed and dissipated also by the output stage of the amp, so more load on the output to be accounted for. This also where the output impedance of the amp comes into play, as that determines the damping factor.
Bottom line, high current amps are in general, a good thing, but not the only thing
|
|
Gosh, glad I could help!😄
Off to read it...
|
@mclinnguy ,
Not hypothetical ones, that’s reserved specifically for us in the flesh he-men!
😎 💪
|
@erik_squires ,
Nice and simple, I actually followed along!
So, an amplifier shouldn't even be called an amplifier. Isn't it just a big fancy switching regulator?
|
@thecarpathian
Well, switching implies binary, and with linear amps the transistors or tubes slide smoothly between the rails.
A faucet, with hot and cold water valves may be a better analogy.
It's still called an amplifier because the input voltage is multiplied. Usually by 20. So your DAC through your preamp puts out +-0.1 V, the amp is going to push out +- 2V.
|
@sns "Not only low impedance but impedance curves matter greatly as well."
Exactly. The issue with the Watts/Amps equation is that it's generally used for power consumption in appliances and such where you have (almost) perfect sine waves.
Speakers are complex loads that change impedance and resistance constantly based on what you're trying to amplify. A simple P = I x E doesn't quite capture that complexity.
The issue for audiophiles is manufacturers never give enough information to evaluate it nor can most people understand it, so you have to do the unthinkable.... Listen to the combination of speaker and amp that you want to use and turn the volume up. Crank it. If it sounds like crap it's probably not a good match for your use.
|
@mulveling Is there a metric (number) for what constitutes a high current amplifier?
|
@tomrk I offered a good metric earlier; whether or not the amp can double power from 4 to 2 Ohms.
|
@panzrwagn +1
simplest test of amp current handling adequacy is to tap low frequency. driver membrane and checking voltage waveform at speaker terminals with the scope.. if voltage amplitude p-p observed is more than 10mV, then need to check speaker connectors, cable, amp relay contacts, and then try higher current amp design to see if it helps! |


